Bubble Sort
Implement a function that performs a bubble sort. The function should take in an array of integers and return an array with the integers sorted in ascending order. The input array is modified.
Examples
bubbleSort([9, 3, 6, 2, 1, 11]); // [1, 2, 3, 6, 9, 11]bubbleSort([12, 16, 14, 1, 2, 3]); // [1, 2, 3, 12, 14, 16]
Recap
Bubble sort is a simple sorting algorithm which compares and swaps adjacent elements such that after every iteration over the array, one more element will be ordered/correctly placed, starting from the largest.
The algorithm starts by iterating over the array, comparing each adjacent pair of elements and swapping them if the larger one is on the left. This will ensure that after one whole iteration, the largest element in the array will be at the last index.
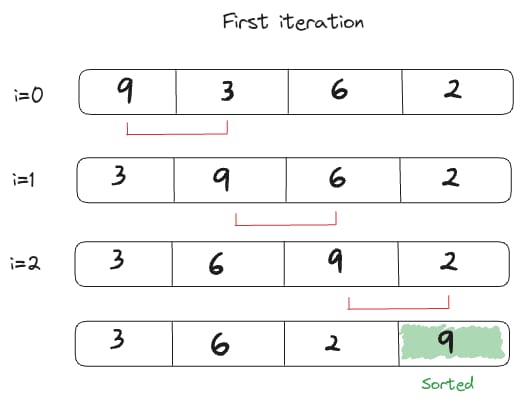
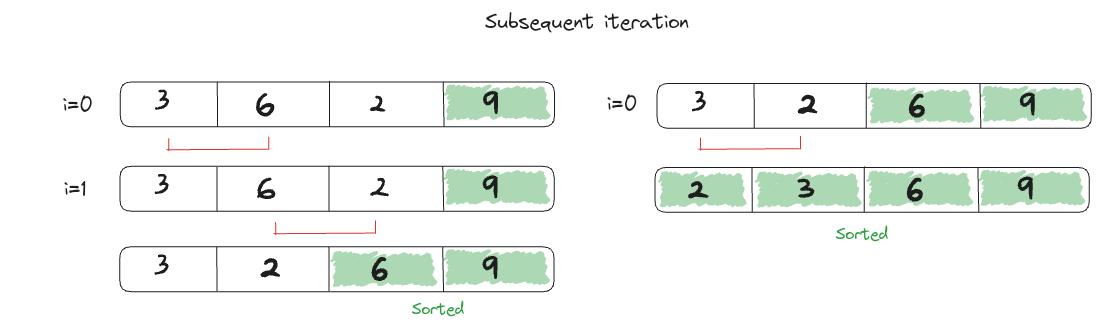
The algorithm then continues to iterate over the array and compares adjacent pairs, such that the 2nd largest element will be at the 2nd last index. The comparison of adjacent pairs can ignore the last element as it is already confirmed to be the largest element in the array through the first iteration.
For e.g., continuing from the algorithm above, the algorithm will move onto the 3rd iteration to compare adjacent pairs while ignoring the last and 2nd last element as they are already in the right order/place.
Premium solution
Purchase premium to unlock official solutions and all the best materials we have to offer.You must be signed in to view your submissions
Loading editor
Loading editor
Loading tests
JavaScript Console
As declaraçõesconsole.log() aparecerão aqui.